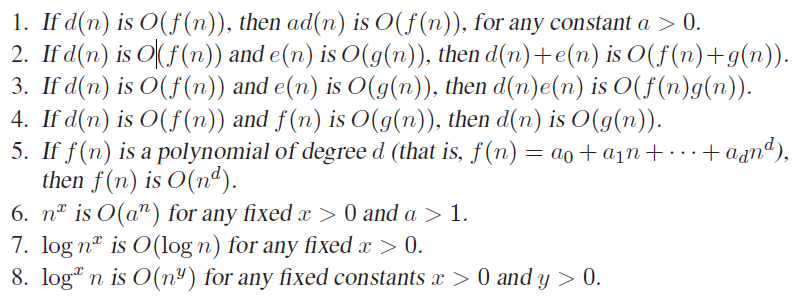Contents
- Big-Oh
- Trær
- Maps og hashing
- Prioritetskø & Heap
- Grafer
- Sortering
- Tekstalgoritmer
- Parallell Sortering
- Kombinatorisk Søking
Big-Oh
Forenklet analyse av en algoritmens effektivitet.
- viser kompleksitet iforhold til N-input størrelse
- maskin uavhengig
- forenkler maskinkode til steg
- viser tid og størrelse
Generelle regler:
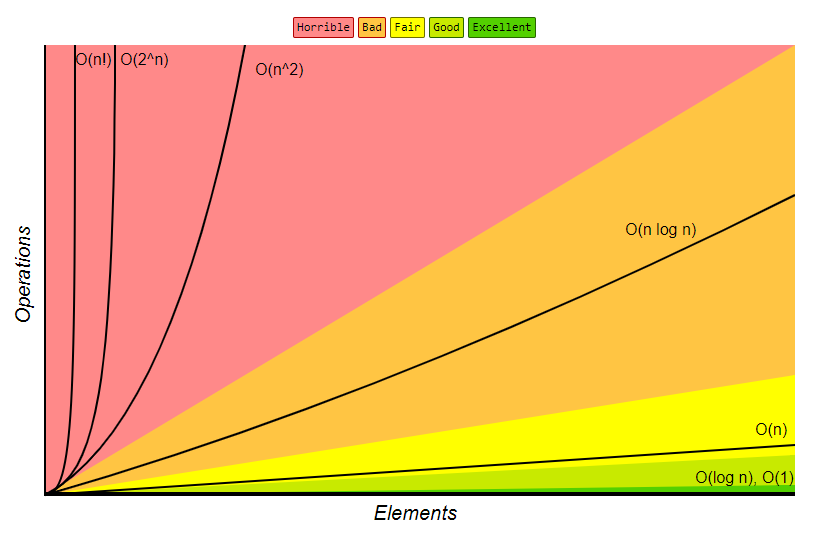
- konstanter ignoreres: 5n -> O(n)
- noen resultater dominerer andre: \(O(1) < O(log n) < O(n) < O(nlog n) < O(n^2) < O(2^n) < O(n!)\)
Flere regler:
Eksempel:
Definisjon:
La \(T(n)\) være kjøretiden til programmet. \(T(n)=O(f(n))\) hvis det finnes positive konstanter \(c\) og \(n_0\) slik at
\(T(n) \leq c * f(n)\) når \(n > n_0\)
\(O(f(n))\) er den øvre grense for kjøretiden.
Oppgaven er å finne \(f(n)\) som er minst mulig.
Trær
Terminologi
- Et tre er en samling noder.
- Et ikke-tomt tre består av en rot-node og null eller flere ikke tomme subtrær.
- Fra roten går det en rettet kant til roten i hvert subtre
- Løvnoder er de ytre/nederste nodene i treet, og indre noder er noder som har barn.
Traversering av et tre består av:
- Leting
- Innsetting
-
Fjerning
- Lengden på en vei er definert som antall kanter på veien.
- Dybden til en node er den unike veien til roten.
- Roten har altså dybde 0
- Rekursiv metode for å beregne dybden til alle nodene i et tre:
void calcDepth(int d){
this.depth = d;
for(Node child : children){
child.calcDepth(d+1);
}
}
- Høyden til en node er definert som lengden av den lengste veien fra noden til en løvnode.
int calcHeight(){
int tmp;
this.height = 0;
for(Node child : children){
tmp = b.calcHeight() + 1;
if(tmp > this.height){
this.height = height;
}
}
retun this.height;
}
Binærtrær
- Hver node har aldri mer enn to barn.
- Dersom det bare er ett subtre, må det være angitt om dette er venstre eller høyre subtre.
class BinNode{
Object element;
BinNode left;
BinNode right;
}
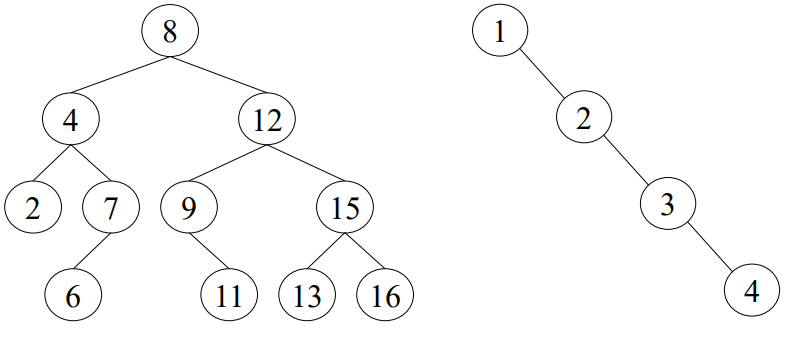
Binære søketrær
- Alle verdiene i venstre subtre er mindre enn verdien i noden selv.
- Alle verdiene i høyre subtre er større enn verdien i noden selv.
- Alle operasjoner tar snittmessig O(log n) tid.
- Gjennomsnittlige dybden er O(log n) når alle innsettingsrekkefølger er like sannsynlige.
- Worst case er O(n) når en operasjon utføres bare langs venstre, eller høyre pekerne i treet. Fungerer da som en liste.
Søking: Rekursiv Metode
Her antar vi at nodene er forskjellige
public BinNode find(Comparable x, BinNode n){
if (n == null){
return null;
}
else if(x.compareTo(n.element) < 0){
return finn(x, n.venstre);
}
else if(x.compareTo(n.element) > 0){
return finn(x, n.hoyre);
}
else{
return n;
}
}
Søking: Ikke-Rekursiv Metode
public BinNode find(Comparable x, BinNode n){
BinNode t = n;
while (t != null && x.compareTo(t.element) != 0){
if (x.compareTo(t.element) < 0){
t = t.venstre;
}
else{
t = t.hoyre;
}
}
return t;
}
Innsetting
- Søk nedover treet på vanlig måte
- Gjør ingenting om elementet finnes
- Sett inn elementet ved første null-peker
Sletting
- Noden er løvnode:
- fjernes direkte
- Noden har bare ett barn:
- Pekeren til foreldernoden endres til barnet til noden
- Noden har to barn:
- Erstatt verdien i noden med den minste verdien i høyre subtre.
- Slett noden som denne minste verdien var i.
Rød-Svarte trær
- Roten = svart
- Hvis noden er rød, er barna svart.
- Alle veier fra en node til en null-peker må inneholde samme antall svarte noder.
- Høyden er da maksimalt \(2log_2(N+1)\)
Innsetting
- Hvis foreldernoden er svart:
- Den nye noden settes inn som rød, antall svarte noder på veien til null-pekerne blir som før.
- Hvis foreldernoden er rød:
- Den nye noden kan ikke være rød (2)
- Den nye noden kan ikke være svart (3)
- Treet må endres ved** hjelp av rotasjoner og omfarging.
- Rotasjoner:
- Zig rotasjon
- Zig-zag rotasjon
- Rotasjoner:
Algoritmen
- Gjør innsetting som i et bst, der den ny noden X farges rød.
- La P og G være forelder og besteforelder til X, og S søsken til P.
- Hvis P er svart: Alt ok, innsetting ferdig.
- Hvis P er rød:
- Hvis X og P begge er venstre/høyre barn: Zig rotasjon med nødvendige fargeendringer.
- Hvis X er venstre og P høyre barn eller motsatt: Zig-zag rotasjon med nødvendige fargeendringer.
- Sett X til å være den nye roten i det roterte subtreet.
- Hvis X nå er roten i selve treet: Farg denne svart, ellers gjenta fra steg 2.
B-trær av orden M
- Brukes når treet ikke får plass i primærminnet.
- Stor bredde
- Balansert
- Typisk for databasesystemer.
Definisjon:
- Data er lagret i løvnoder.
- Interne noder lagrer inntil M-1 nøkler for søking: nøkkel i angir den minste verdien i subtre i+1.
- Roten er
- enten løvnode
- eller har mellom 2 og M barn
- Alle andre indre noder har mellom [M/2] og M barn.
- Alle løvnoder har samme dybde.
- Alle løvnoder har mellom [L/2] og L dataelementer eller datapekere.
Søking etter x
- Start i roten.
Tidsforbruk
- Antar at M(indre) og L(løv) er omtrent like.
- Siden hver indre node unntatt roten har minst M/2 barn, er dybden til B-treet maksimalt \(log_(M/2)N\)
- For hver node må vi utføre \(O(log M)\) arbeid(binærsøk) for å avgjør hvilken gren vi skal gå til.
- Dermed tar søking \(O(lov M*log_(M/2)N = O)\) tid.
- Ved innsetting og sletting kan det hende at vi må gjøre
Maps og hashing
Abstrakte datatyper
- Består av:
- Et sett med objekter
- Spesifikasjon av operasjoner på disse.
- Eksempler:
- Binært søketre
- innsetting
- søking
- fjerning
- Mengde
- union
- snitt
- finn
- Map
- containsKey
- get
- put
- Binært søketre
Map
- Samling nøkler-, verdi-par.
- Nøkler er unike
- Typiske operasjoner:
- containsKey(key)
- get(key)
- put(key, value)
- keySet()
- values()
- SortedMap - Nøkler organisert i sortert orden.
Hashing
- Lagrer elementer i arrays.
- Nøkkelen -> Hash-funksjon -> Indeks
- En god hash-funksjon:
- er rask å beregne
- gir alle mulige verdier fra 0 til tableSize - 1
- fordeler bra utover indeksene
- En hashtabell tilbyr konstant gjennomsnittstid ved:
- Innsetting
- sletting
- søking
- NB! La alltid tabellstørrelsen være et primtall.
Hash-funksjoner
Eksempel: Strenger som nøkler(1):
int hash1(String key, int tableSize){
int hashVal = 0;
for(int i = 0; i < key.length(); i++){
hashVal += key.charAt(i);
}
return(hashVal % tableSize);
}
Denne er enkel å implementere, men gir forholdsvis dårlig fordeling ved store tabellstørrelser.
Eksempel: Strenger som nøkler(2):
int hash2(String key, int tableSize){
int hashVal = key.charAt(0) +
27 * key.charAt(1) +
729 * key.charAt(2);
return(hashVal % tableSize);
}
Denne gir grei fordeling for tilfeldige strenger, men språk er som regel ikke tilfeldig.
Eksempel: Strenger som nøkler(3):
\(\sum_{i=0}^{keySize-1} key[keySize-i-1]*37^i\)
int hash3(String key, int tableSize){
int hashVal = 0;
for(int i = 0; i < key.length(); i++){
hashVal = 37*hashVal + key.charAt(i);
}
return Math.abs(hashVal % tableSize);
}
Denne er rask å beregne, med god fordeling. Kan dog være noe lang beregningstid for lange nøkler.
Oppsummering:
- Må teoretisk kunne gi alle mulige verdier fra 0 til tableSize - 1.
- Må gi en god fordeling utover tabellindeksene.
- Generelt så bør hashen/indeks-basen være mange ganger tabellstørrelsen før modulus(%) utføres.
Kollisjonhåndtering
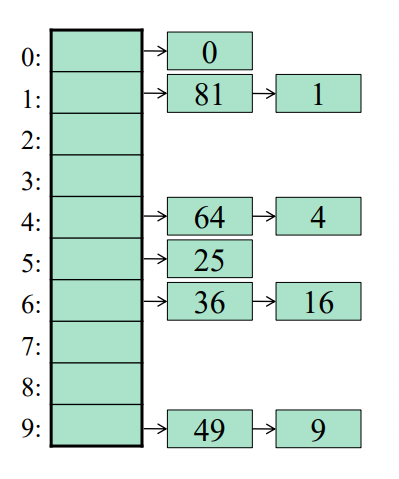
- Åpen hashing:
- Elementer med samme hash-verdi samles i en struktur(liste).
- Load-faktoren \(\lambda\) ønskes å være tilnærmet lik 1. Altså antall elementer iforhold til tabellstørrelsen.
- Lukket hashing:
- Er en indeks opptatt, prøv igjen til en ledig blir funnet.
- Her ønsker man en load-faktor på ca \(\lambda \approx 0.5\)
Strategier for lukket-hashing
Prøver alternative indekser \(h_i(x)\) inntil vi finner en som passer.
h_i(x) = (hash(x) + f(i)) mod tableSize
- Lineær prøving
- \(f(i) = i\)
- Kvadratisk prøving
- \(f(i) = i^2\)
- Dobbel hashing
- Bruker en ny hash-funksjon for å løse kollisjonene.
- \(f(i) = i*hash_2(x)\)
- \(hash_2(x) = R - (x mod R)\)
- hvor R er et primtall mindre enn tableSize
- Rehashing
- Hvis tabellen blir for full, tar operasjonene veldig lang tid.
- En mulig løsning er da å opprette en dobbelt så stor tabell. For å så rehashe, elementene i den opprinnelige tabellen i den nye.
- Operasjonen er dyr(O(n)), men opptrer sjeldent.
- Man må ha hatt n/2 innsettinger siden forrige Rehashing.
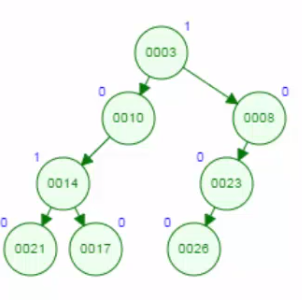
Utvidbar hashing
- Metode for å forhindre overdreven diskaksessering.
- Hash-funksjonen angir hvilken diskblokk elementene befinner seg i.
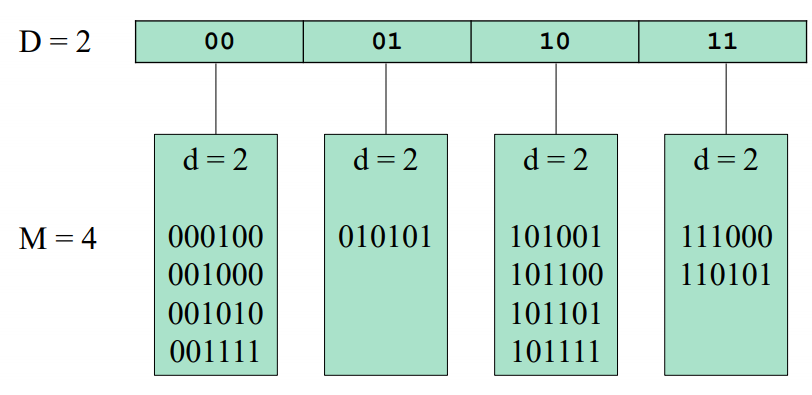
- Katalogen har \(2^D\) indekser
- Hver diskblokk har plass til M elementer.
- For hver diskblokk L lagrer vi et tall \(d_L \leq D\)
- Tallet d(local depth) beskriver antall LSB elementene har til felles(i eksempelet brukes MSB)
Innsettingsalgoritme
- Beregn hash(x) og finn riktig diskblokk L ved å slå opp i katalogen på de D første sifrene i hashverdien.
- Hvis det er færre enn M elementer i L, sett x inn i L.
- Hvis L derimot er full, sammenlign \(d_L\) med D:
- Dersom \(d_L\) < D splitter vi L i to blokker L1 og L2
- Sett \(d_{L1} = d_{L2} = d_L +1\)
- Gå gjennom elementene i L og plasser dem i L1 eller L2 avhengig av verdien på de \(d_l + 1\) første sifrene.
- Prøv igjen å sette inn x (gå til punkt 2).
- Dersom \(d_L = D\):
- Doble katalogstørrelsen ved å øke D med 1.
- Fortsett som ovenfor (splitt L i to blokker osv.)
- Dersom \(d_L\) < D splitter vi L i to blokker L1 og L2
Prioritetskø & Heap
Prioritetskø
- Lav tall = høy prioritet
- Må minst ha
insert(x,p)ogdeleteMin() - Mest brukte datastruktur er Heap grunnet gunstig O-notasjon.
Binær Heap (Heap)
- Strukturkrav: En binær heap er et komplett binærtre
- Ordningskrav: Barn er alltid større eller lik sine foreldre
Strukturkrav komplett binærtre
- Treet må være i perfekt balanse
- Bladnoder vil ha høydeforskjell på maks 1
- Treet med høyden h har mellom \(2^h\) og \(2^{(h+1)}-1\) noder
- Den maksimale høyden på treet vil være \(log_2(n)\)
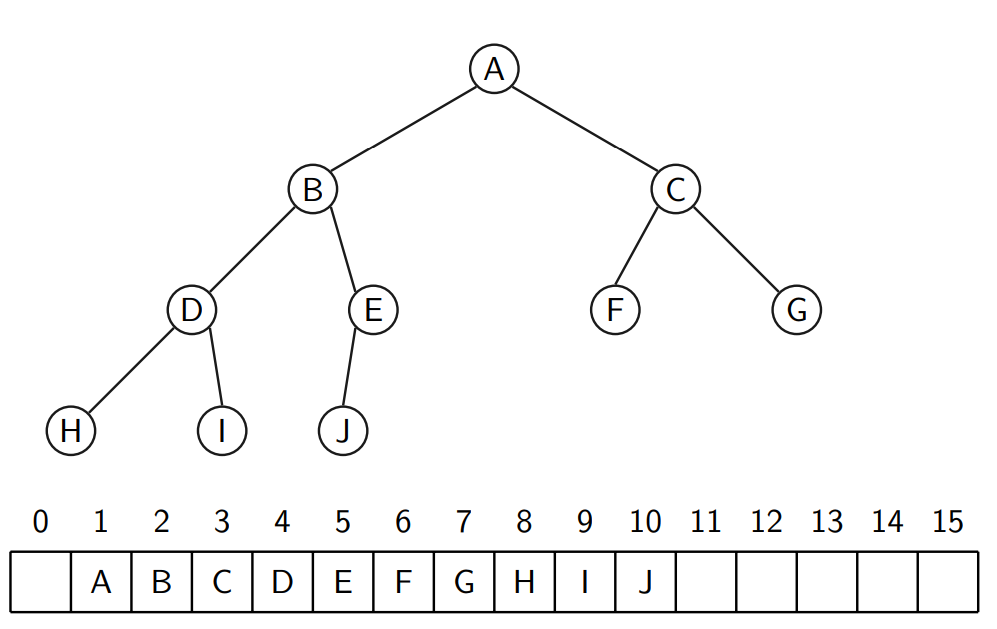
Representasjon
- Siden binærtreet er komplett kan vi legge elementene i en array
- Finn elementer:
- Venstre barn: \(index * 2\)
- Høyre barn: \(index * 2 + 1\)
- Foreldre: (int) \(index/2\)
insert
- Legg elementet på neste ledige plass i heapen
- La elementet flyte opp
- Dette tar \(O(log_2(n))\)
deleteMin
- Fjern rot elementet(det minste)
- La det siste elementet bli ny rot
- La den nye roten flyte til riktig posisjon
- Maks flyt er \(O(log_2(n))\)
Andre Operasjoner
findMinkan gjøres i \(O(0)\)deletefjern vilkårlig element fra heapen- Kan gjøres ved
decreaseKey\(\infty\) +deleteMin
- Kan gjøres ved
- Endring av prioritet på elementer:
- Senking:
increaseKey - Øking:
decreaseKey - Gjøres typisk ved å:
- Lokalisere element i heapen
- Øk eller senk prioritet
- La elementet flyte opp eller ned
- Senking:
Sortering
- Vi kan bygge en binær heap (
insert) på \(O(n*log_2(n))\) - Vi kan ta ut alle elementene (
deleteMin) \(O(n*log_2(n))\)
Venstreorientert Heap
- Variant av binær heap
- Ordningskrav: samme som ordningskravet til binær heap
- Strukturkrav:
- La
null_path_length(x)være lengden av korteste veien fra x til en node uten to barn. npl(l)\(\geq\)npl(l)hvor l og r er venstre og høyre barnet til x- Forsøker å være ubalansert
- La
- Å flette to binære heaper (
merge) tar Θ(N) for heaper med like størrelser - Venstreorientert Heap støtter merge i \(O(log n)\)
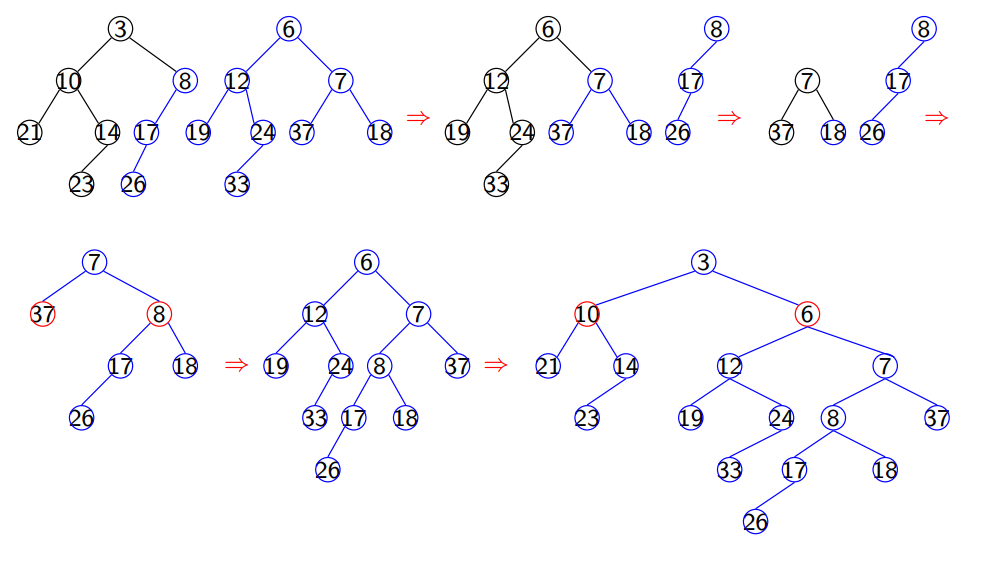
Merge
- Kan gjøres rekursivt:
- sammenligner H1.rot med H2.rot. Antar nå at H1.rot er minst.
- la den høyre subheapen til H1 være heapen som man får ved å merge H1.høyre med H2
- bevare strukturkravet ved å bytte ut (swap) rotens høyre og venstre barn.
Huffman-koding
- Datakompresjon av tekstfiler
- Hovedidé:
- Tegn som forekommer ofte = korte koder, sjeldne tegn = lange koder
- Regel 1: Hvert tegn som forekommer i filen, skal ha sin egen entydige kode
- Regel 2: Ingen kode er prefiks i en annen kode
- Eksempel: a = 011001, da kan ikke 0, 01, 011, 0110 eller 01100 være koder for tegn
Algoritme
- Lag en frekvenstabell for alle tegn som forekommer i datafilen
- Betrakt hvert tegn som en node, og legg dem inn i en prioritetskø P med frekvensen som vekt
- Mens P har mer enn ett element
- Ta ut de to minste nodene fra P
- Gi dem en felles foreldrenode med vekt lik summen av de to nodenes vekter
- Legg foreldrenoden inn i P
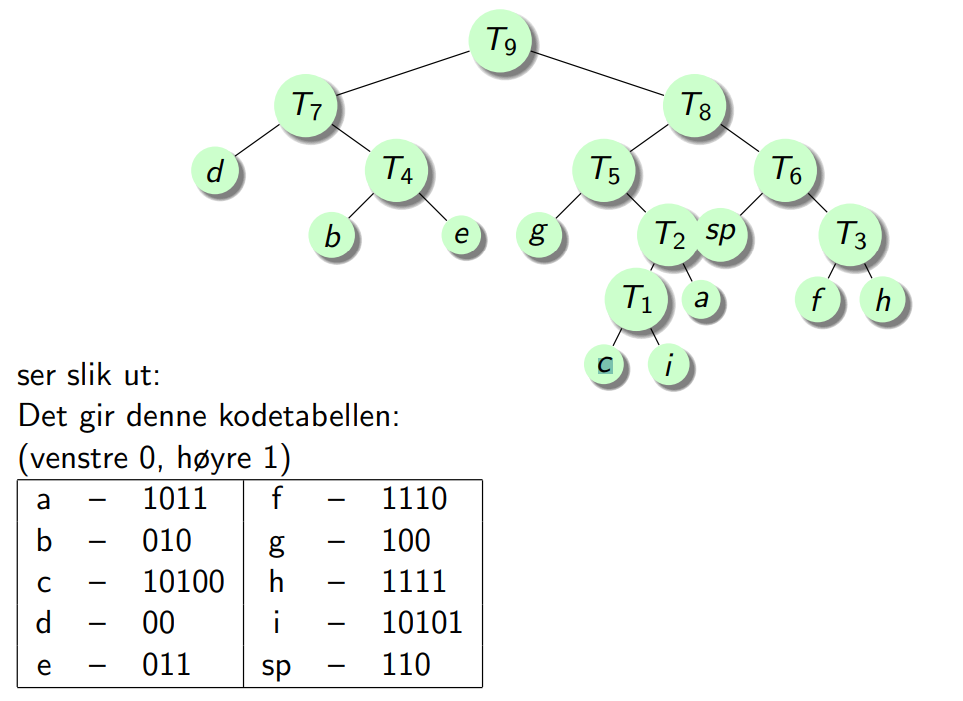
- Huffmankoden til et tegn (bladnode) får vi ved å går fra roten og gi en ‘0’ når vi går til venstre og ‘1’ når vi går til høyre
- Resultatfilen består av to deler:
- I En tabell over Huffmankoder med tilhørende tegn
- Den Huffmankodede datafilen
Eksempel:
Grafer
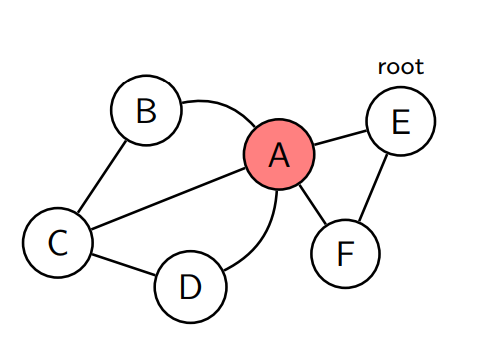
Definisjon
- En graf G =(V,E) har en mengde noder, V, og en mengde kanter, E
-
V og E er henholdsvis antall noder og antall kanter i grafen - Hver kant er et par av noder, dvs. \((u, v)\) slik at \(u, v \in V\)
- En kant (u, v) modellerer at u er relatert til v
- Dersom nodeparet i kanten (u, v) er ordnet (dvs. at rekkefølgen har betydning), sier vi at grafen er rettet, i motsatt fall er den urettet
- “Alt” kan modelleres med grafer
- Node y er nabo-node (eller etterfølger) til node x dersom \((x, y) \in E\)
- En graf er vektet dersom hver kant har en tredje komponent, kalt kost eller vekt
- En vei (eller sti) i en graf er en sekvens av noder \(v_1, v_2, v_3, . . . , v_n\) slik at \((v_i , v_i+1) \in E\) for \(1 \leq i \leq n − 1 \)
- Lengden til veien er lik antall kanter på veien, dvs. n − 1
- Kosten til en vei er summene av vektene langs veien
- En vei er enkel dersom alle nodene (untatt muligens første og siste) på veien er forskjellige
- En løkke (sykel) i en rettet graf er en vei med lengde \(\geq 1\) slik at \(v_1 = v_n\). Løkken er enkel dersom stien er enkel
- I en urettet graf må også alle kanter i løkken være forskjellige
- En rettet graf er asyklisk dersom den ikke har noen løkker
- En rettet, asyklisk graf blir ofte kalt en DAG (Directed, Acyclic Graf)
- En urettet graf er sammenhengende dersom det er en vei fra hver node til alle andre noder
- En rettet graf er sterkt sammenhengende dersom det er en vei fra hver node til alle andre noder
- En rettet graf er svakt sammenhengende dersom den underliggende urettede grafen er sammenhengende
- Graden til en node i en urettet graf er antall kanter mot noden
- Inngraden til en node i en rettet graf er antall kanter inn til noden
- Utgraden til en node i en rettet graf er antall kanter ut fra noden
Representasjon
- Nabo-matrise (adjacency matrix)
- Bra hvis “tett” graf, dvs \(E = O(V^2)\)
- Det tar \(O(V)\) tid å finne alle naboer
- Nabo-liste (adjacency list)
- Bra hvis “tynn” (“sparse”) graf
- Tar \(O(\text{Utgrad}(v))\) tid å finne alle naboer til v
- De fleste grafer i det virkelige liv er tynne
- Objekter & array
- Grafer også representeres ved en kombinasjon av node-objekter og etterfølgerarrayer
- Arraylengden kan være en parameter til node-klassens constructor
- Da må vi vite antall etterfølgere når vi genererer noden
- Eventuelt kan vi estimere en øvre grense og la siste del av arrayen være tom
- Vi trenger da en variabel som sier hvor mange etterfølgere en node faktisk har
class Node{
int antallNaboer;
Node[] etterf;
double[] vekt;
Node(int kapasitet){
etterf = new Node[kapasitet];
vekt = new double[kapasitet];
antallNaboer = 0;
}
}
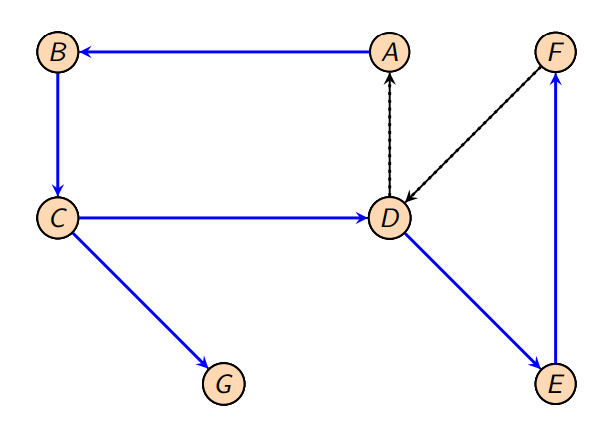
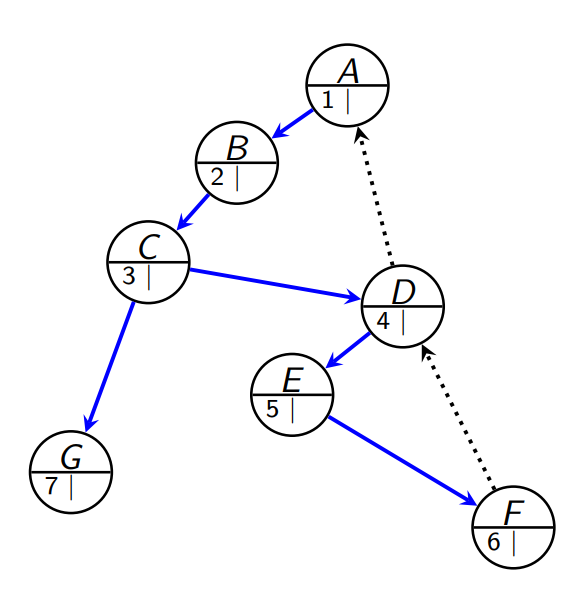
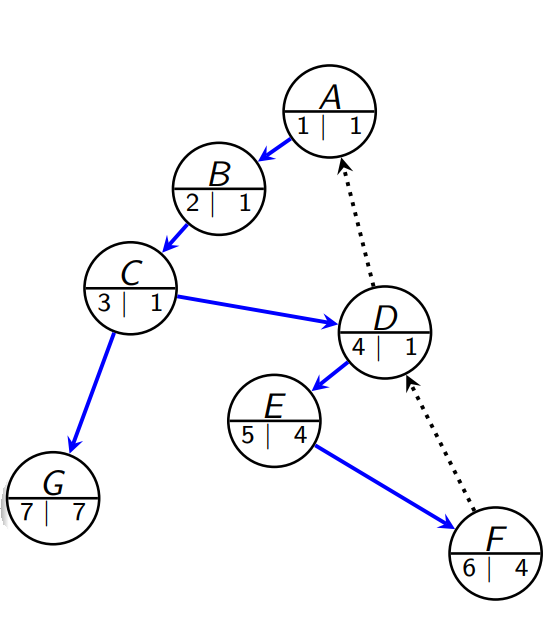
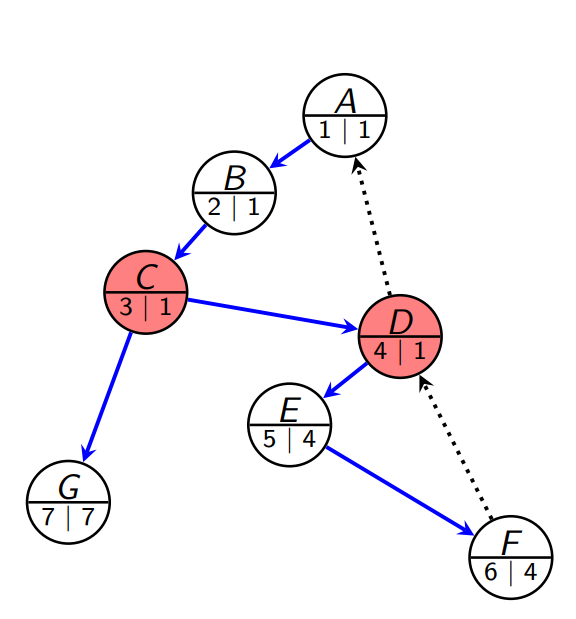
Topologisk sortering
- En topologisk sortering er en ordning (rekkefølge) av noder i en DAG slik at dersom det finnes en vei fra vi til \(v_j\) , så kommer \(v_j\) etter vi i ordningen
- Topologisk sortering er umulig hvis grafen har en løkke
Algoritme
- Finn en node med inngrad = 0
- Skriv ut noden, og fjern noden og utkantene fra grafen (marker noden m ferdig og reduser inngraden til nabonodene)
- Gå tilbake til punkt 1
void topsort(){
Node fokusNode;
for(int i = 0; i < ANTALL_NODER; i++){
fokusNode = finnNodeInngradNull();
if(fokusNode == null){
error("Løkke funnet!");
}
else{
< Skriv ut fokusNode som node 'i'>
for(Node nabo : fokusNode.Naboer){
nabo.inngrad--;
}
}
}
}
- Denne algoritmen er \(O(V^2)\) siden finnNodeInngradNull ser gjennom hele node/inngrad-tabellen hver gang
- Unødvendig: bare noen få av verdiene kommer ned til 0 hver gang
void topsortBetter(){
Node fokusNode;
LinkedList<Node> inngradNullStack = new LinkedList<Node>();
int i = 0;
for(Node node : Noder){
if(node.inngrad == 0){
inngradNullStack.add(node);
}
}
while(!inngradNullStack.isEmpty()){
fokusNode = inngradNullStack.removeFirst();
< Fjern fra graf og skriv ut fokusNode som node 'i'>
i++;
for(Node nabo : fokusNode.Naboer){
nabo.inngrad--;
if(nabo.inngrad == 0){
inngradNullStack.add(nabo);
}
}
}
if(i < ANTALL_NODER){
error("Loop found!");
}
}
- Forutsatt at vi bruker nabolister, er denne algoritmen \(O(V + E)\).
- Kø/stakk-operasjoner tar konstant tid, og hver node og hver kant blir bare behandlet en gang.
Korteste vei, en-til-alle
Uvektet graf:
- Korteste vei fra s til t i en uvektet graf er lik veien som bruker færrest antall kanter.
Bredde-først algoritme
- Følgende bredde-først algoritme løser problemet for en node s i en uvektet graf G:
- Marker at lengden fra s til s er lik 0. merk at s foreløpig er den eneste noden som er markert.)
- Finn alle etterfølgere til s. marker disse med avstand 1.
- Finn alle umarkerte etterfølgere til nodene som er på avstand 1. marker disse med avstand 2.
- Finn alle umarkerte etterfølgere til nodene som er på avstand 2. marker disse med avstand 3.
- Fortsett til alle noder er markert, eller vi ikke har noen umarkerte etterfølgere.
- Finnes det fortsatt umarkerte noder, kan ikke hele G nåes fra s.
- Hvis G er urettet, skjer dette hvis og bare hvis G er usammenhengende.
void uvektet(Node s){
for(Node v : alleNoder){
v.avstand = UENDELIG;
v.kjent = false;
}
s.avstand = 0;
for(int dist=0; dist < ANTALL_NODER; i++){
for(Node v : alleNoder){
if(!v.kjent && v.avstand == dist){
v.kjent = true;
for(Node nabo : v.naboNoder){
if(nabo.avstand == UENDELIG){
nabo.avstand = dist+1;
nabo.vei = v;
}
}
}
}
}
}
Hovedløkken vil som oftest fortsette etter at alle noder er merket, men den vil terminere selv om ikke alle noder kan nåes fra s. Tidsforbruket er \(O(V^2)\)
void uvektetBetter(Node s){
LinkedList<Node> k = new LinkedList<>();
Node fokusNode;
for(Node n : alleNoder){
n.avstand = UENDELIG;
}
s.avstand = 0;
k.add(s);
while(!k.isEmpty()){
fokusNode = k.removeFirst();
for(Node nabo : fokusNode.naboNoder){
if(nabo.avstand == UENDELIG){
nabo.avstand = fokusNode.avstand+1;
nabo.vei = fokusNode;
k.add(nabo);
}
}
}
}
- Vi sparer tid ved å benytte en kø av noder.
- Vi begynner med å legge s inn i køen.
- Så lenge køen ikke er tom, tar vi ut første node i køen, behandler denne og legger dens etterfølgere inn bakerst i køen.
- Da blir s behandlet først. Så blir alle noder i avstand 1 behandlet før alle i avstand 2, før alle i avstand 3 . . .
- Denne strategien ligner på bredde først traversering av trær (først rotnoden, så alle noder på nivå 1, så alle noder på nivå 2, osv).
- Tidsforbruket blir \(O(E + V)\) fordi køoperasjoner tar konstant tid og hver kant og hver node bare blir behandlet en gang.
- Bruken av kø gjør attributtet kjent overflødig.
- Forutsatt at vi bruker nabolister, er denne algoritmen \(O(V + E)\).
- Kø-operasjoner tar konstant tid, og hver node og hver kant blir behandlet bare en gang.
Djikstra
Vektet graf, uten negative kanter
Algoritme
- For alle noder: Sett avstanden fra startnoden s lik ∞. Merk noden som ukjent
- Sett avstanden fra s til seg selv lik 0
- Velg en ukjent node v med minimal (aktuell) avstand fra s og marker v som kjent
- For hver ukjent nabonode w til v:
- Dersom avstanden vi får ved å følge veien gjennom v, er kortere enn den gamle avstanden til s
- reduserer avstanden til s for w
- sett bakoverpekeren i w til v
- Dersom avstanden vi får ved å følge veien gjennom v, er kortere enn den gamle avstanden til s
- Akkurat som for uvektede grafer, ser vi bare etter potensielle forbedringer for naboer (w) som ennå ikke er valgt (kjent)
Uvektet: \(d_w = d_v+1\) hvis \(d_w = \infty\)
Vektet: \(d_w = d_v+c_{v,w}\) hvis \(d_v + c_{v,w} < d_w\)
Tidsforbruk
- Hvis vi leter sekvensielt etter den ukjente noden med minst avstand tar dette \(O(V)\) tid, noe som gjøres \(V\) ganger, så total tid for å finne minste avstand blir \(O(V^2)\)
- I tillegg oppdateres avstandene, maksimalt en oppdatering per kant,
- dvs. til sammen \(O(E)\)
- Totalt tidsforbruk: \(O(E + V^2) = O(V^2)\)
Raskere implementasjon(for tynne grafer):
- Bruker en prioritetskø til å ta vare på ukjente noder med avstand mindre enn ∞
- Prioriteten til ukjent node forandres hvis vi finner kortere vei til noden
- deleteMin og decreaseKey bruker \(O(log V)\) tid
Vektet graf, med negative kanter
Mulig løsning:
- Nodene er ikke lenger kjente eller ukjente
- Vi har i stedet en kø som inneholder noder som har fått forbedret avstandsverdien sin
- Løkken i algoritmen gjør følgende:
- Ta ut en node v fra køen
- For hver etterfølger w, sjekk om vi får en forbedring \((d_w > d_v + c{v,w})\)
- Tidsforbruket blir \(O(E · V)\)
- Det finnes ingen korteste vei med negative løkker i G. Det er det hvis og bare hvis samme node blir tatt ut av køen mer enn V ganger. Da må vi terminere algoritmen.
Vektet graf, asykliske grafer
- Lineær tid ved å behandle nodene i en topologisk rekkefølge: \(O(E · V)\)
- når en node v er valgt, kan \(d_v\) ikke lenger senkes siden det er ingen innkommende kanter som kommer fra ukjente noder
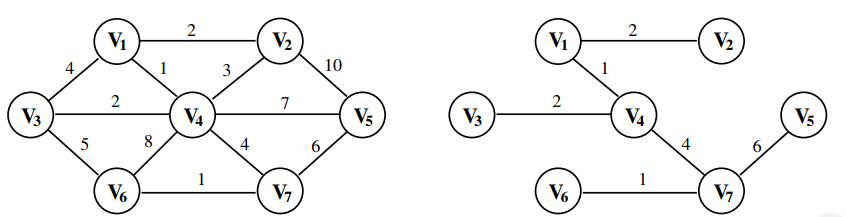
Minimale spenntrær
- Et minimalt spenntre for en urettet graf G er et tre med kanter fra grafen, slik at alle nodene i G er forbundet til lavest mulig kostnad
- eksisterer bare for sammenhengende grafer
- Generelt: flere minimale spenntrær for samme graf
Grådige Algoritmer
Prims algoritme
- Bygger et minimalt spenntre
- Treet bygges opp trinnvis, I hvert trinn: pluss en kant (og dermed en tilhørende node) til treet
- 2 typer noder:
- Noder som er med i treet
- Noder som ikke er med i treet
- Nye noder: velge en kant (u, v) med minst vekt slik at u er med i treet, og v ikke er det.
- Algoritmen begynner med å velge en vilkårlig node
- Samme kjøretid som for Dijkstra
Kruskals algoritme
- Se på kantene en etter en, sortert etter minst vekt
- Kanten aksepteres hvis, og bare hvis, den ikke fører til noen løkke
- Algoritmen implementeres vha. en prioritetskø og disjunkte mengder:
- Initielt plasseres kantene i en prioritetskø og nodene i hver sin disjunkte mengde (slik at find(v) gir mengden til (v)).
- deleteMin gir neste kant (u, v) som skal testes
- Hvis find(u) ! = find(v), har vi en ny kant i treet og gjør union(u, v)
- Hvis ikke, ville (u, v) ha dannet en løkke, så kanten forkastes
- Algoritmen terminerer når prioritetskøen er tom, eventuelt når vi har lagt inn \(V − 1\) kanter
Tidsanalyse
- Hovedløkken går E ganger
- I hver iterasjon gjøres en deleteMin, to find og en union, med samlet tidsforbruk: \(O(log E) + 2·O(log V)+O(1) = O(log V)\) (fordi \(log E < 2 · log V\) )
- Totalt tidsforbruk er O(E · log V)
Prim vs. Kruskal
- Prims algoritme er noe mer effektiv enn Kruskals, spesielt for tette grafer
- Prims algoritme virker bare i sammenhengende grafer
- Kruskals algoritme gir et minimalt spenn-tre i hver sammenhengskomponent i grafen
Dybde-først søk
- generalisering av prefiks traversering for trær
- gitt: start node v: rekursivt traverserer alle nabonodene
- rekursjon \(\rightarrow\) vi undersøker alle noder som kan nåes fra første etterfølger til v, før vi undersøker neste etterfølger til v
- for vilkårlige grafer: pass på å terminere rekursjon! \(\rightarrow\) unvisited ↔ visited nodes.
Algoritmen
- Initialize: all nodes “unvisited”
- Recur:
- when visited: return immediately
- when unvisited
- set to visited
- recur on all neighbors
void dfs(Node v){
v.merke = true;
for(Node nabo : v.naboer){
if(!w.merke){
dfs(w);
}
}
}
Løkkeleting
- Vi kan bruke dybde-først søk til å sjekke om en graf har løkker
- 3 verdier til tilstandsvariablen: usett, igang og ferdig (besøkt)
void findLoop(Node v){
if(v.status = "running"){
<Loop found>
}
else if(v.status == "idle"){
v.status = "running";
for(Node n : v.neighbors){
findLoop(n);
}
v.status = "done";
}
}
Grafens tilstand
- Hvis grafen ikke er sammenhengende, kan vi foreta nye dybde-først søk fra noder som ikke er besøkte, inntil alle nodene er behandlet
urettet graf & DFS
- En urettet graf er sammenhengende hvis og bare hvis et dybde-først søk som starter i en tilfeldig node, besøker alle nodene i grafen
rettet graf & DFS
- En rettet graf er sterkt sammenhengende hvis og bare hvis vi fra hver eneste node v klarer å besøke alle de andre nodene i grafen ved et dybde-først søk fra v
Urettet grafer
Dybde-først-spenntre
- for urettet sammenhengende grafer
- ikke sammenhengende grafer: dfs spanning forest
- huske “back-pointers”
- Ulike typer kanter:
- tree edges - tilhører treet
- back edges - tilhører ikke treet
Biconnectivity
En sammenhengende urettet graf er bi-connected hvis det ikke er noen noder som ved fjerning gjør at grafen blir ikke sammenhengende. Slik node heter cut-vertices eller articulation point.
Er grafen bi-connected?
- DFS-spenntre - Konstruer et dfs spenntre fra en node v av G.
- Alle kantene (v, w) i G er representert i treet som enten en tree edge eller som en back edge
- Nummerer nodene når vi besøker dem
- Low-number - for hver node i treet: beregn low-nummeret
- laveste noden som kan nås ved å ta 0 eller flere tree edge etterfulgt av 0 eller 1 back edge
- Dette gjør vi like før vi trekker oss tilbake (idet vi er ferdig med kallet)
- note: på dette tidspunktet har funnet low for alle barna til noden
- Cut-vertex - En node v er en cutvertex i G hvis:
- v er rotnoden av \(DFS_G\)-treet og har to eller flere tree edges
- v ikke er rotnoden av \(DFS_G\) og det finnes en tree edge (v, w) slik at low(w) \(\geq\) num(v)
Rot
Roten av DFS-treet er en cutvertex hvis den har to eller flere utgående tree edges.
- tilbaketrekking må gå gjennom roten for å komme fra den ene til den andre sub-treet.
Ikke-rot node
Et ikke-rot node v er en cutvertex hvis den har et barn w slik at ingen back edge som starter i subtreet av w når en predesessornode til v.
void dfs(Node v){
v.num = counter++;
v.status = visited;
for(Node w: v.adjacentNodes){
if(w.status != visited){
w.parent = v;
}
dfs(w);
}
}
void assignlow(Node v){
v.low = v.num;
for(Node w: v.adjacentNodes){
if(w.num > v.num){
assignlow(w);
if(w.low >= v.num){
System.out.println(v + "an articulation point!");
}
v.low = min(v.low, w.low);
}
else{
if(v.parent != w){
v.low = min(v.low, w.num);
}
}
}
}
Strongly Connected Components
Rettet graf & dfs
En rettet graf er sterkt sammenhengende hvis og bare hvis vi fra hver eneste node v klarer å besøke alle de andre nodene i grafen ved et dybde-først søk fra v
Definisjon
Gitt en rettet graf G = (V, E). En strongly connected component av G er en maksimal sett av noder \(U \subseteq V\) slik at for alle \(u_1, u_2 \in U\) vi har at \(u_1 \rightarrow* u_2\) and \(u_2 \rightarrow* u_1\).
Hvis vi kan nå alle noder og alle noder kan nå v, så kan alle nå alle ved å gå gjennom v.
Sortering
- Hva avgjør tidsforbruket ved sortering
- Sorteringsalgoritmen
- N, antall elementer vi sorterer
- Fordelingen av disse (Uniform, skjeve fordelinger, spredte,..)
- Effekten av caching
- Optimalisering i jvm (Java virtual machine) også kalt >java
- Parallell sortering eller sekvensiell
JIT-kompilering
- Programmet optimaliseres (omkopmileres) under kjøring flere ganger av optimalisatoren i JVM (java) stadig raskere.
- Første gang en metode kjøres, oversettes den fra Byte-kode til maskinkode
- Blir den brukt flere/mange ganger optimaliseres denne maskinkoden i en eller flere steg (minst 2 steg)
- Denne prosessen kalles JIT (Just In Time)-kompilering
- God idé: kode som brukes mye skal gå raskest mulig
- Det er nå over 100 programmeringsspråk (også Python, som Jython) som bruker JVM dette gjelder da alle disse språkene, ikke bare Java.
Tidtaking med JIT-kompilatoren
double [] tider = new double[numIter];
//nHigh = 10mill, nLow= 100, nstep = 10, numIter = 3 eller helst 5
for (n = nHigh; n >= nLow; n= n/nStep){
for (med = 0; med < numIter; med++) {
long t = System.nanoTime(); // start tidtagning i nanosek.
// kode du tar tider på;
tider[med] = (System.nanoTime()-t)/1000000.0; // millisek.
}
}
Sorterings problemet
- Kaller arrayen a[] før sorteringen og a’[ ] etter
- Sorteringskravet
- Stabil sortering
- To like elementer vil beholde den samme rekkefølgen.
- Sorteringsalgoritmene må virke hvis er to (eller fler) like verdier i a[ ]
- I testkjøringene antar vi at innholdet i a[] er en tilfeldig trukne tall mellom 0 og n-1. Dette betyr at også etter all sannsynlighet er dubletter (to eller flere like tall) som skal sorteres , men ikke så veldig mange.
- Hvor mye ekstra plass bruker algoritmen
- Bevaringskriterietlle elementene vi hadde i a[], skal være i a’[]
Sammenligning-baserte sorteringsalgoritmer:
Baserer seg på sammenligning av to elementer i a[]:
- Innstikk
- Boble
- Shellsort
- TreeSort
- Quicksort
Bubblesort
Bytt om naboer hvis den som står til venstre er størst, lar den minste boble venstreover
void bytt(int[] a, int i, int j)
{ int t = a[i];
a[i] = a[j];
a[j] = t;
}
void bobleSort (int [] a)
{int i = 0;
while ( i < a.length-1)
if (a[i] > a[i+1]) {
bytt (a, i, i+1);
if (i > 0 ) i = i-1;
} else {
i = i + 1;
}
}
Innstikk sortering (n < 50)
Idé: Ta ut ut element a[k+1] som er mindre enn a[k]. Skyv elementer k, k-1,… ett hakk til høyre til a[k+1] kan settes ned foran et mindre element.
void insertSort(int[] ){
int i, t, max = a.length -1;
for(int k = 0; k < max; k++){
if(a[k] > a[k+1]){
t = a[k+1];
i = k;
do{
a[i+1] = a[i];
i--;
} while(i >= 0 && a[i] > t);
a[i] = t;
}
}
}
- Fungerer ofte som en hjelpe algoritme
Verdi-baserte sorteringsalgoritmer:
Direkte plassering basert på verdien av hvert element – ingen sammenligninger med nabo-elementer e.l.
- Bøtte
- VenstreRadix og HøyreRadix
Radix algoritmer
- To typer:
- RR: fra høyre og venstre-over (vanligst iterativ og rask) RR: 12345
- LR: fra venstre og høyre-over (rask - rekursiv ) LR: 12345
Algoritmene:
- Begge: Finner først max verdi i a [ ]
- = bestem største siffer i alle tallene
- Tell opp hvor mange elementer det er av hver verdi på det sifferet (hvor mange 0-er, 1-ere, 2-..) man sorterer på
- Da vet vi hvor 0-erne skal være, 1-erne skal være, etter sortering på dette sifferet ved å addere disse antallene fra 0 og oppover.
- Flytter så elementene i a[] direkte over til riktig plass i b[]
Høyre-radix-sortere på to siffer:
static void radix2(int [] a) {
// 2 digit radixSort: a[ ]
int max = 0, numBit = 2;
// finn max = største verdi I a[]
for (int i = 0 ; i <= a.length; i++){
if (a[i] > max) max = a[i];
}
// bestemme antall bit i max
while (max >= (1<<numBit)) numBit++;
int bit1 = numBit/2, // antall bit i første siffer
bit2 = numBit-bit1; // antall bit i andre siffer
int[] b = new int [a.length];
radixSort( a,b, bit1, 0);
radixSort( b,a, bit2, bit1);
}
static void radixSort (int [] a, int [] b, int maskLen, int shift){
int acumVal = 0, j;
int mask = (1<<maskLen) -1;
int [] count = new int [mask+1];
// 1) count[]=the frequency of each radix value in a
for (int i = left; i <=right; i++)
count[(a[i]>> shift) & mask]++;
// 2) Add up in 'count' - accumulated values
for (int i = 0; i <= mask; i++) {
j = count[i];
count[i] = acumVal;
acumVal += j;
}
// 3) move numbers in sorted order a to b
for (int i = 0; i < a.length; i++)
b[count[(a[i]>>shift) & mask]++] = a[i];
}
Shell-Sortering \(O(n^2)\)
- Den virker fordi når gap = 1 fungere den som en Innstikksort.
- Den er vanligvis raskere fordi vi har nesten sortert a[] før gap=1. Når a[] er delvis sortert, sorterer innstikksortering meget kjapt.
- Worst case som med innstikk: \(O(n^2)\)
- Mye raskere med andre, lure valg av verdier for gap \(O(n^{3/2})\) eller bedre:
- Velger primtall i stigende rekkefølge som er minst dobbelt så store som forgjengeren + n/(på de samme primtallene): \((1,2,5,11,23...., n/23, n/11, n/5, n/2)\)
- Meget lett å lage sekvenser som er betydelig langsommere enn Shells originale valg, f.eks bare primtallene.
- En slik sekvens begynner på 1
Shell2 – en annen sekvens for gap
void Shell2Sort(int [] a)
{ int [] gapVal = {1,2,5,11,23, 47, 101, 291, n/291, n/101,n/47,n/23,n/11,n/5,n/2 };
int gap;
for (int gapInd = gapVal.length -1; gapInd >= 0; gapInd --) {
gap = gapVal[gapInd];
for (int i = gap ; i < a.length ; i++)
if (a[i] < a[i-gap] ) {
int tmp = a[i],
j = i;
do
{ a[j] = a[j-gap];
j = j- gap;
} while (j >= gap && a[j-gap] > tmp);
a[j] = tmp;
}
}
}
MaxSort (\(O(n^2)\))
void maxSort ( int [] a) {
int max, maxi;
for ( int k = a.length-1; k >= 0; k--){
max = a[0]; maxi=0;
for (int i = 1; i <=k; i++) {
if (a[i] > max) {
max = a[i];
maxi =i;}
}
bytt(k, maxi);
} // end for k
} // end maxSort
void bytt (int k, int m){
int temp = a[k];
a[k] = a[m];
a[m] = temp;
}
Tre og Heap-sortering
- Rota er største element i treet (også i rota i alle subtrær – rekursivt)
- Det er ingen ordning mellom vsub og hsub (hvem som er størst)
- Vi betrakter innholdet av en array a[0:n-1] slik at vsub og hsub til element ’i’ er i: ’2i+1’ og ’2i+2’ (Hvis vi ikke går ut over arrayen)
Idé (Heap &) Tre sortering
- Tre – sortering:
- Vi starter med røttene, i først de minste subtrærne, og dytter de ned (får evt, ny større rotverdi oppover)
- Heap-sortering:
- Vi starter med bladnodene, og lar de stige oppover i sitt (sub)-tre, hvis de er større enn rota.
- Felles:
- Etter denne første ordningen, er nå største element i a[0]
Tre sortering
void dyttNed (int i, int n) {
// Rota er (muligens) feilplassert
// Dytt gammel nedover
// få ny større oppover
int j = 2*i+1, temp = a[i];
while(j <= n )
{ if ( j < n && a[j+1] > a[j] ) j++;
if (a[j] > temp) {
a[i] = a[j];
i = j;
j = j*2+1;
}
else break;
}
a[i] = temp;
} // end dyttNed
void treeSort( int [] a)
{ int n = a.length-1;
for (int k = n/2 ; k > 0 ; k--) dyttNed(k,n);
for (int k = n ; k > 0 ; k--) {
dyttNed(0,k); bytt (0,k);
}
}
Analyse av tree-sortering
- Den store begrunnelsen: Vi jobber med binære trær, og ’innsetter’ i prinsippet n verdier, alle med vei \(log_2 n\) til \(rota = O(n log n)\)
- Først ordner vi n/2 subtrær med gjennomsnittshøyde = (log n) / 2 = n * logn/4
- Så setter vi inn en ny node ’n’ ganger i toppen av det treet som er i a[0..k], k = n, n-1,..,2,1. I snitt er høyden på dette treet (nesten) log n dvs n log n.
- Summen er klart O(n logn)
Heap-Sortering
void dyttOpp(int i)
// Bladnoden på plass i er
// (muligens) feilplassert
// Dytt den oppover mot rota
{ int j = (i-1) / 2,
temp = a[i];
while( temp > a[j] && i > 0 ) {
a[i] = a[j];
i = j;
j = (i-1)/2;
}
a[i] = temp;
} // end dytt OPP
void heapSort( int [] a) {
int n = a.length -1;
for (int k = 1; k <= n ; k++)
dyttOpp(k);
bytt(0,n);
for (int k = n-1; k > 0 ; k--) {
dyttNed(0,k);
bytt (0,k);
}
}
Analyse av Heap -sortering
- Som Tre-sortering: Vi jobber med binære trær (hauger) , og innsetter i prinsippet n verdier, alle med vei \(log_2\) til \(rota = O(n log n)\)
Quicksort
Idé
- Finn ett element i (den delen av) arrayen du skal sorter som er omtrent ’middels stort’ blant disse elementene kall det ’part’
- Del opp arrayen i to deler og flytt elementer slik at:
- små - de som er mindre enn ’part’ er til venstre
- like - de som har samme verdi som ’part’ er i midten
- store - de som er større, til høyre
- Gjennta pkt. 1 og 2 rekursivt for de små og store områdene hve for seg inntil lengden av dem er < 2, og dermed sortert.
void quicksort ( int [] a, int left, int right)
{ int i= l, j=r;
int t, part = a[(left+right)/2];
while ( i <= j) {
while ( a[i] < part ) i++; //hopp forbi små
while (part < a[j] ) j--; // hopp forbi store
if (i <= j) {
// swap en for liten a[j] med for stor a[i]
t = a[j];
a[j]= a[i];
a[i]= t;
i++;
j--;
}
}
if ( left < j ) { quicksort (a,left,j); }
if ( i < right ) { quicksort (a,i,right); }
} // end quickSort
Tidsforbruk
- Vi ser at ett gjennomløp av quickSort tar \(O( r-l )\) tid, og første gjennomløp \(O(n)\) tid fordi \(r-l = n\) første gang
Verste tilfellet
Vi velger ’part’ slik at det f.eks. er det største elementet hver gang. Da får vi totalt n kall på quickSort , som hver tar \(O(n/2)\) tid i gj.snitt – dvs \(O(n^2)\) totalt
Beste tilfellet
Vi velger part slik at den deler arrayen i to like store deler hver gang. Treet av rekursjons-kall får dybde log n. På hvert av disse nivåene gjennomløper vi alle elementene (høyst) en gang dvs: \(O(n) + O(n) + ... +O(n) = O (n log n)\) ( log n ledd i addisjonen)
Gjennomsnitt
I praksis vil verste tilfellet ikke opptre – men kan velge ’part’ som medianen av \(a[l], a[(l+r)/2\) og \(a[r]\) og vi får ‘alltid’ \(O(n*log(n))\)
Quicksort i praksis
- Valg av partisjoneringselement ’part’ er vesentlig
- Quicksort er ikke den raskeste algoritmen (f.eks er Radix minst dobbelt så rask), men Quicksort nyttes mye – f.eks i java.util.Arrays.sort();
- Quicksort er ikke stabil (dvs. to like elementer i inndata kan bli byttet om i utdata)
Lamoto Quicksort
void lamotoQuick( int[] a, int low, int high) {
// only sort arrayseggments > len =1
int ind =(low+high)/2, piv = a[ind];
int storre=low+1, // hvor lagre neste 'storre enn piv'
mindre=low+1; // hvor lagre neste 'mindre enn piv'
bytt (a,ind,low); // flytt 'piv' til a[lav] , sortér resten
while (storre <= high) {
// test iom vi har et 'mindre enn piv' element
if (a[storre] < piv) {
// bytt om a[storre] og a[mindre], få en liten ned
bytt(a,storre,mindre);
++mindre;
} // end if - fant mindre enn 'piv'
++storre;
} // end gå gjennom a[i+1..j]
bytt(a,low,mindre-1); // Plassert 'piv' mellom store og små
if ( mindre-low > 2) lamotoQuick (a, low,mindre-2); // sortér alle <= piv
// (untatt piv)
if ( high-mindre > 0) lamotoQuick (a, mindre, high); // sortér alle > piv
} // end sekvensiell Quick
Fordeler:
- Meget enklere å få riktig
- Litt langsommere, men lett optimaliseres ved å legge inn flg. linjer hvis det er flere like elementer i a[]:
int piv2 = mindre-1; while (piv2 > low && a[piv2] == piv) { piv2--; // skip like elementer i midten }
Merge sort
- Velegnet for sortering av filer og data i primær minnet. ####
Generell idé:
- Vi har to sorterte sekvenser (eller arrayer) A og B (f.eks på hver sin fil)
- Vi ønsker å få en stor sortert fil C av de to.
- Vi leser da det minste elementet på ’toppen av’ A eller B og skriver det ut til C, ut-fila
- Forsett med pkt. 3. til vi er ferdig med alt.
- Rask, men krever ekstra plass.
- Kan kodes rekursivt med fletting på tilbaketrekking.
I praksis skal det meget store filer til, før du bruker flettesortering 16 GB intern hukommelse er i dag meget billig (noen få tusen kroner) Før vi begynner å flette, vil vi sortere filene stykkevis med f.ek Radix, Kvikk- eller Bøtte-sortering
Psudo
Algoritme fletteSort ( innFil A, innFil B, utFil C)
{
a = A.first;
b = B. first;
while ( a!= null && b != null)
if ( a < b) { C.write (a); a = A.next;}
else { C.wite (b); b = B.next;}
while (a!= null) { C.write (a); a = A.next;}
while ( b!= null) { C.write (b); b = B.next;}
}
Stabilitet
- Innstikk: stabil
- Quick: ikke stabil
- HRadix: stabil
- VRadix: ikke stabil, men kan sette stabil
- TreSort: ikke stabil
- MaxSort: ikke stabil, avhengig av:
if (a[i] > max)ellerif(a[i] >= max) - Flette: ikke nødvendigvis stabil
Oppsummering:
- Mange sorteringsmetoder med ulike egenskaper (raske for visse verdier av n, krever mer plass, stabile eller ikke, spesielt egnet for store datamengder,…)
- Algoritmer:
- Boblesort : bare dårlig (langsomst)
- Innstikksort: raskest for \(n < 0 – 50\)
- Maxsort – langsom, men er et grunnlag for Heap og Tre
- Tre-sortering: Interessant og ganske rask : \(O(n*log(n))\)
- Quick: rask på middelstore datamengder (ca. n = 50 -5000)
- Radix-sortering: Klart raskest når n > 500 , men HøyreRadix trenger mer plass (mer enn n ekstra plasser – flytter fra a[] til b[] + count[])
Tekstalgoritmer
Algoritmer for lokalisering av substrenger:
- Brute force
- Enkleste tenkelige algoritme for å løse problemet
- Boyer Moore Horspool
- Relativt komplisert algoritme, med rask worst case
Bouyer Moore
- Boyer Moore antar at vi bare har 1-byte characters
- 1-byte characters gir oss 256 muligheter
- Vi kan bruke den informasjonen til å preprosessere nålen
- Vi matcher baklengs med Boyer Moore
Enkel sudo kode:
BouyerMoore(String H, String N) //H has n characters, N has m characters
i = m-1
j = m-1
repeat
if N[j] = H[j]
if j = 0
return i //a match
else
//last() char returns -1 if not found
i = i + m - min(j, 1 + last(H[i]))
j = m-1
until i > n-1
return -1;
Bad Character Shift(Forenklet)
Preprosseserer nåla, lager en array med “skift” lengde på alle karakterer bortsett i fra de i nåla. “Skift” lengden er lengden til nåla på de som ikke er elementer i nåla.
int[] badCharShift = new int[256]; // assume 1-byte characters
for(int i = 0; i < badCharShift.length; i++){
badCharShift[i] = needle.length;
}
/* shift size = 1 for characters inside needle */
for(int i = 0; i < needle.length; i++){
badCharShift[ (int) needle[i] ] = 1;
}
Boyer Moore Horspool
public int boyer moore horspool(char[] needle, char[] haystack){
if ( needle.length > haystack.length ){ return -1; }
int[] bad shift = new int[CHAR MAX]; // 256
for(int i = 0; i < CHAR MAX; i++){
bad shift[i] = needle.length;
}
int offset = 0, scan = 0;
int last = needle.length - 1;
int maxoffset = haystack.length - needle.length;
for(int i = 0; i < last; i++){
bad shift[needle[i]] = last - i;
}
while(offset <= maxoffset){
for(scan = last; needle[scan] == haystack[scan+offset]; scan--){
if(scan == 0){ // match found!
return offset;
}
}
offset += bad shift[haystack[offset + last]];
}
return -1;
}
Horspool er en forenkling av Boyer-Moore-streng-søkealgoritmen
Boyer-Moore-algoritmen er basert på:
- analysere nålen baklengs
- bad character shift
- good suffix shift
- bad character shift unngår å gjenta mislykkede sammenligninger mot et tegn i høystakken
- good suffix shift beregner hvor langt vi kan flytte nålen, basert på antall matchende bokstaver før mismatch
- justerer bare matchende nål-tegn mot høystakk-tegn som allerede har fått match
- good suffix shift er en array som er like lang som nålen
Good suffix shift
Good suffix shift er et hopp som prøver å matche en tidligere del av søkestrengen mot det vi allerede har klart å matche opp mot slutten, så vidt dette er mulig. Altså den tar utgangspunkt i det matchende suffikset (good suffix) for hvor langt vi skal hoppe.
Parallell Sortering
- Vi vil ha raskere algoritmer, også sortering
- Vi har nå flere prosessorkjerner, burde bruke alle disse.
Amdahls lov
- Med p% sekvensiell kode er det raskeste du kan forbedre din algoritmen din er 100/p ganger (eks. 100/20 =5).
- Uansett hvordan du parallelliserer og uansett hvor mange maskiner du har, fordi den parallelle koden kan aldri gå raskere enn på 0,000.. sekunder.
- Den sekvensielle delen vil derfor alltid gi deg en begrensning, og må gjøres minst mulig.
- Med k prosessorer er mulig Speedup (= ganger raskere), S:
- \[S \leq \frac{100}{p + \frac{100-p}{k}}, \quad S \leq 3.33 \; \text{med p} = 20, k = 8\]
- Dette er ikke nødvendigvis sannheten. Gustafson (med sin lov) hevder at den sekvensielle %-andelen ofte synker når problemet blir større. Amdahl er ikke fasit sier Gustafson.
Noen Problemer
- Trådene kan flette beregninger
- Kompilatoren bytter om på instruksjonene
- Cachen gjør at ulike tråder kan lese ’gamle’ verdier av variable lenge etter at de er oppdatert i en annen tråd.
- Det tar ’lang’ tid, ca. 3 millisekunder å starte noen få tråder (på den tida kan man sortere ca. 10-40 000 tall)
Synkroniseringsvariable generelt
- Tråder som skal synkroniseres, gjør et kall på samme synkroniseringsvariabel (barrier, lock eller semafor) – i samme objekt. Da skjer:
- Alle instruksjoner ’over’ synkroniserings-kallet i koden vil bli ferdig utført før synkroniseringskallet – ingen utsatte operasjoner.
- Alle verdier på felles variable som er endret av trådene vil være tilgjengelig og synlig i felles hukommelse nå kallet blir utført.
- Dvs. innholdet i alle cachene som har blitt endret, blir skrevet ned i hovedhukommelsen som et resultat av kall på en synkroniseringsvariabel.
Kombinatorisk Søking
Sekvens-generering
class Gen{
int[] p;
int n;
Gen(int i){
n = i;
p = new int[n];
}
void gen(int plass){
for (int siffer = 0; siffer < n; siffer++) {
p[plass] = siffer;
if (plass < n - 1) {
gen(plass + 1);
} else {
for(int i = 0; i < n; i++){
System.out.println(p[i]);
}
System.out.println("\n");
}
}
}
}
Permutasjoner
class Gen{
int[] p;
int n;
boolean[] brukt;
Gen(int i){
n = i;
p = new int[n];
brukt = new boolean[n];
for(int j = 0; j < n; j++){
brukt[j] = false;
}
}
void gen(int plass){
for (int siffer = 0; siffer < n; siffer++) {
if(!burkt[siffe]){
brukt[siffe] = true;
p[plass] = siffer;
if(plass < n-1){
gen(plass + 1);
}
else{ <Lever p til videre bruk.> }
brukt[siffer] = false;
}
}
}
}
Direkte generering av permutasjoner
void permuter(int i) {
if (i == n – 1) {
< Lever p til videre bruk. >
} else {
permuter(i + 1);
for (int k = i + 1; k < n; k++) {
bytt(i,k);
permuter(i + 1);
}
roterVenstre(i);
}
}
void bytt(i,j) {
int tmp = p[i];
p[i] = p[j];
p[j] = tmp;
}
void roterVenstre(int i) {
int tmp = p[i];
for (int k = i + 1; k < n; k++) {
p[k – 1] = p[k];
}
p[n-1] = tmp;
}
Kombinatorisk søking:
- Har: Et endelig antall elementer.
- Skal: Finne en rekkefølge, gjøre et utplukk, lage en oppdeling,..
Vi må da:
- Lage alle interessante kombinasjoner.
- Teste om en kombinasjon er en løsning på det aktuelle problemet.
NB! Ofte slår vi disse sammen, slik at vi bare lager kombinasjoner som er potensielle løsninger.